| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- computerscience
- 국비지원
- 야놀자
- 너비우선탐색
- 프론트엔드개발자
- BFS
- 컴퓨터과학
- 그리디
- 코테
- CS
- nodejs
- 국비지원취업
- html/css/js
- 패스트캠퍼스
- CSS
- cpu
- 알고리즘
- 자바스크립트
- 부트캠프
- github
- 호이스팅
- 백준
- js
- KAKAO
- 코딩테스트
- LinkSnap
- DFS
- git
- Javascript
- 컴퓨터공학
- Today
- Total
My Boundary As Much As I Experienced
수학 복습 시작합니다. (코테 풀다가 느낀 수학 개념의 필요성) 본문
일단 긴 얘기부터 해보겠다. 수학공부를 하고싶게 된 이유에 대한 얘기다.
코테를 풀다보면 수학적인 개념이 나올 때가 종종 있다.
어제는 어린 왕자라는 문제를 풀었는데, '이게 실버3이야?' 할 정도로 고난이도의 문제로 느껴졌다.
'최소 골드 하위 문제 같은데..'라는 생각이 들었다. 문제를 보자면,

- 어린 왕자의 위치와 장미의 위치, 그리고 행성계의 좌표가 주어진다.
- 위 사진에서 자유곡선의 왼쪽 끝이 어린왕자의 위치고 오른쪽 끝이 장미이다.
- 위 사진에서 동심원들로 표시된게 행성계이다.
- 행성계는 중첩되어 있을 수 있다. 그러나 애매하게 일부 교집합이 있는채로 있다거나 하진 않는다.
이때, '어린왕자가 장미를 만나러 가려면 얼마나 많은 행성계를 가로질러야하는가?' 가 문제였다.
좌표는 -1000부터 +1000까지의 X, Y좌표로 구성되어있다.
나는 이 문제를 풀기 위해서 여러 시도를 해봤는데, 기본적으론 일단 2차원 배열로 전체 맵을 만든 후
좌표마다 객체를 넣고, 객체 안에 해당 좌표가 어떤 행성계에 포함되는지, 어린왕자가 있는 곳인지, 장미가 있는 곳인지 등을 마킹하려고 했다.
// 전체 맵의 형태(2차원 배열에 각각 정보 저장용 객체):
[
[{ ... }, { ... }, { ... }, { ... }, { ... }, { ... }, { ... }, { ... }, ...],
[{ ... }, { ... }, { ... }, { ... }, { ... }, { ... }, { ... }, { ... }, ...],
[{ ... }, { ... }, { ... }, { ... }, { ... }, { ... }, { ... }, { ... }, ...],
]
만약 어린 왕자가 좌표 x: 10, y: 10에 있다고 치자.
그리고 x: 10, y: 10 좌표는
x좌표: 9, y좌표: 9, 반지름: 4인 행성계와
x좌표: 10, y좌표: 10, 반지름: 5인 행성계에도 속해있게 된다.
그렇다면 x: 10, y: 10 좌표의 정보 저장용 객체는 아래와 같게 구성된다.
// 10, 10 좌표에 있는 객체의 상태:
{
prince: true,
planetBoundary: [ `9_9_4`, `10_10_5` ]
}
이런 식으로 행성계들 마킹, 어린왕자 좌표 표시, 장미 좌표 표시를 2차원 배열에 모두 한 다음에
어린왕자 좌표의 객체와 장미 좌표의 객체만 비교해보면 답을 찾을 수 있을 것이라 생각했다.
이렇게 같은 행성계에 있는 경우는 행성계를 가로지르지 않고도 만날 수 있으니 제외하고, 서로 다른 행성계에 있는 것의 수를 계산하면 정답!
... 일것이라고 생각했지만..!
// 어린왕자 좌표 객체
{
prince: true,
planetBoundary: [ `9_9_7`, `10_10_5` ]
}
// 장미 좌표 객체
{
rose: true,
planetBoundary: [ `9_9_7`, `12_12_2` ]
}
// 9_9_7는 둘 다 포함되어있으니까 행성계를 가로지르지 않기에 빼준다.
그런데 이때 생각해보니 문제가 몇 개 있었다.
첫번째로
어떤 행성계 좌표가 x: 0, y: 0, r: 4라고 할때,
나는 아래처럼 x-4 ~ x+4, y-4 ~ y+4까지 모두 'x_y_4' 행성계로 마킹하려고 했다.
즉 이러면 행성계 모양이 네모 박스가 된다😂.. 하지만 문제에선 분명히 행성계는 동심원 모양이라고 했다.
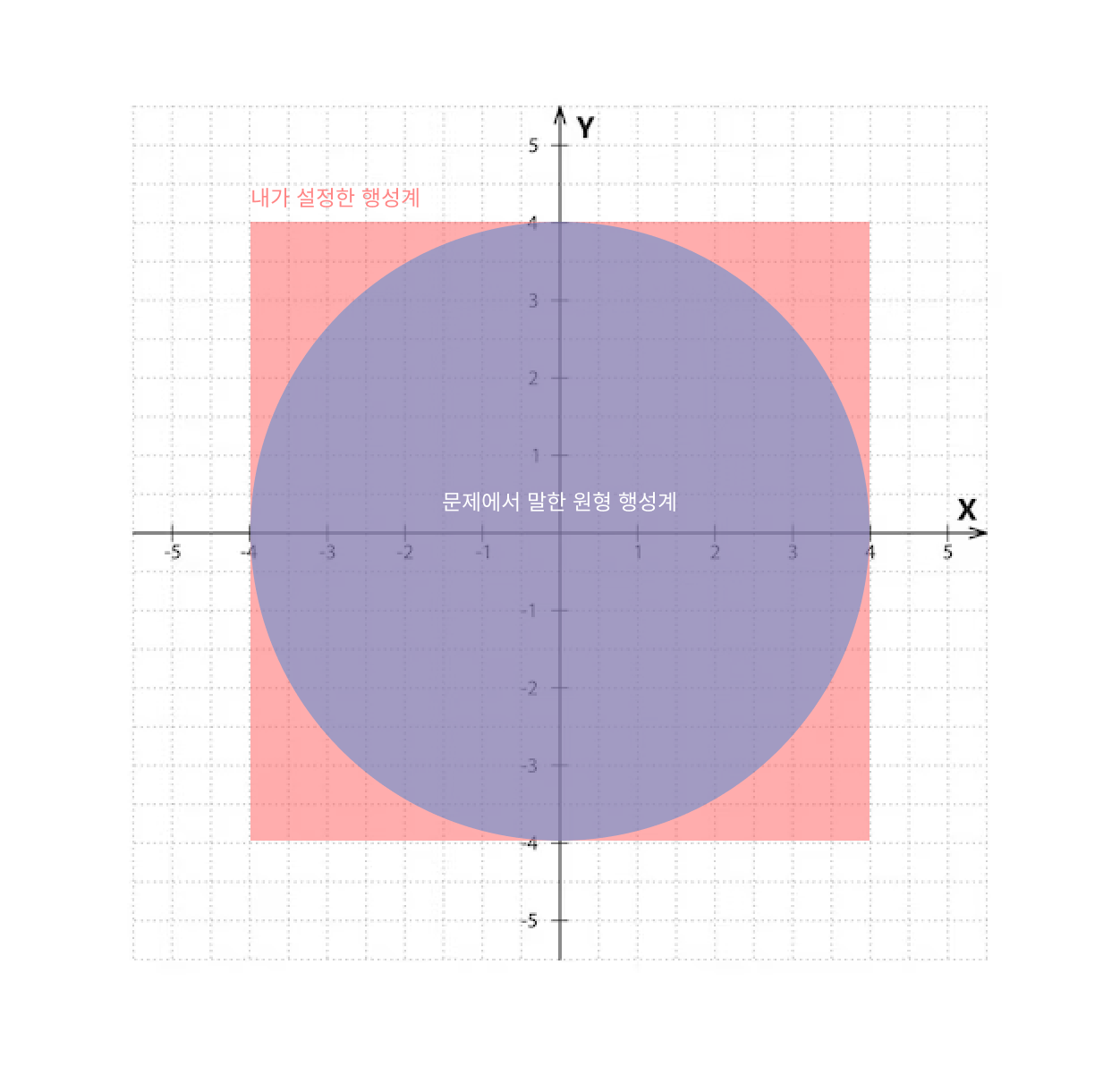
그렇다면 동그란 행성계 원형을 만들려면 어떻게 하는가?
나는 기껏해야 다이아 모양◆밖에 구현할 생각이 나지 않았다.. 이것도 기울인 네모일 뿐이다.
이렇게 네모 모양이면 네모의 각 꼭지점은 동심원 반지름 r보다 훨씬 더 먼 곳이 될텐데..
이 정도 오차는 무시해도 되게 테스트케이스를 짜놨을지 확신이 들지 않았다.
// 내가 행성계를 마킹할 때 썼던 로직
for ( let i = x-9; i < x+9; i++ ) {
for ( let j = y - 9; j < y+9; j++ ) {
// x-9 ~ x+9, y-9 ~ y+9까지 모두 'x_y_9' 행성계로 마킹
}
}
두 번째로
문제에서 주어진 전체 맵 크기가 X, Y 모두 -1000 ~ 1000까지로, 2001 x 2001 사이즈이다. 엄청나게 거대하다.
이 정도 2차원 배열을 구현하려고 하면 백퍼 메모리 오버플로우 실패가 뜬다🤯
그래서 전체 맵 만들기는 포기하고, 아래처럼 객체에 좌표X, Y를 '_'로 구분한 키값을 만들에서 여기에 정보들을 저장하는 것으로 구조를 바꿨다.
{
"9_9" : {
prince: true,
planetBoundary: [ ... ]
},
"9_10" : {
planetBoundary: [ ... ]
},
...
}
이런 식으로 구현해서 채점한 결과 메모리 부족 문제는 안 발생했지만, 결과는 실패!!
테스트 케이스 3개중 2개는 통과하는데 1개는 답보다 +1 높게 나오더라.
아마 정확히 반지름을 지키는 동심원꼴이 아니라 네모꼴 행성계로 범위를 부정확하게 만들어서
원래라면 포함되지 않아야하는 좌표가 장미에 하나 늘었던거 같다.
그래서 더 이상 고민해봤자 더 좋은 답을 찾긴 어려울거 같아서 다른 사람 답안을 참고했는데,
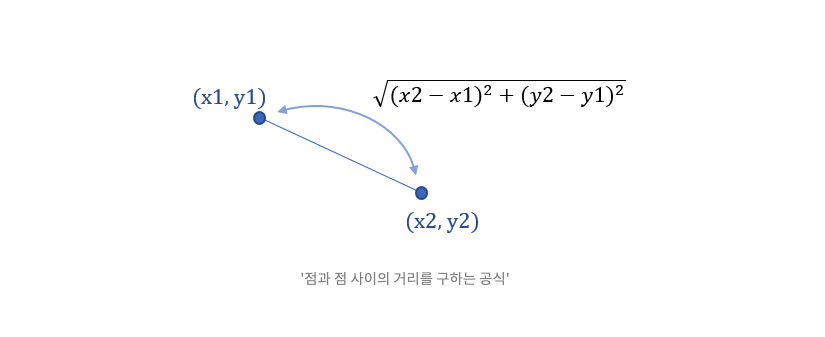
두 점 사이의 거리 공식을 활용하는 것을 알 수 있었다.
이렇게 하면 어떤 좌표가 반지름 내인지 아닌지를 더 정확하게 판별할 수 있겠다.
수학 공식을 잘 까먹지 않고 기억하는 사람은 위와 같은 해결책을 빠르게 생각해냈겠지만,
나는 환상의 2차원 배열 그리기 쇼를 하고 있었다. 역시 아는 것이 힘이다..
내가 3시간 푼 문제가 저 공식 하나만으로 난이도가 엄청 내려가다니 신기했고
더 좋은 해결책들을 찾기 위해선 수학을 잘 알고 있는 것이 중요하다는 것을 느끼게 해줬다.
혹자는 '코테에 나오는 수학문제들 풀어서 뭐하냐? 코테는 실제 개발과 달라 블라블라~' 라고 할수도 있는데...
상관 없다. 코테는 재밌기 때문이다. 내 친구들 리그오브레전드하는 시간은 안 아까워 하는거보면
코테하려고 수학 개념 복습하는건 더욱더 아까운 시간이 아닐테다.
그리고 코테든 수학문제든 뭐든 복잡한 문제를 해결하기위해 끙끙대는 과정에서
원초적인 문제해결능력 자체가 단련된다고 믿는다.
하여튼 수학 공부를 해서 수학 개념이 나오는 코테도 잘 풀고 그래서 pccp같은 알고리즘 자격증도 따고,
나중에 게임 개발할 때도 쓸려고 한다.
